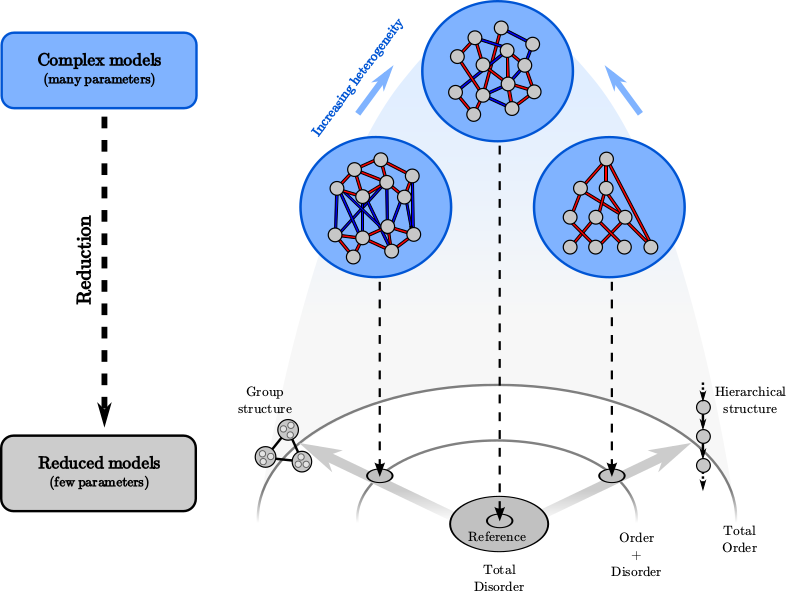
Traditional theoretical ecology describes low-dimensional patterns (few species, few traits...) used as archetypes for intuition. Network models combine many such patterns into more complex systems, but this comes with hard empirical challenges: predictions are sensitive to the whole structure of species interactions, and this structure is difficult to measure precisely and exhaustively.
New approaches, inspired by statistical mechanics, try to make more general predictions on these high-dimensional systems. The underlying assumption is that large systems that have emerged through many concurrent processes, rather than being precisely designed (or co-evolved), tend to exhibit only properties that are most robust to changes in structure. Such robust properties can easily be captured in null models such as random interactions, stochastic dynamics, etc. Hence a different, collective kind of simplicity appears at the other end of complexity.
Our questions are: